Author: Joaquim Peiró (Imperial College London, UK), David Moxey (University of Exeter, UK), Michael Turner (Imperial College London, UK), Gianmarco Mengaldo (California Institute of Technology, USA), Rodrigo C. Moura (Instituto Tecnológico de Aeronáutica, Brazil), Ayad Jassim (Hewlett Packard Enterprise, UK), Mark Taylor (London Computational Solutions, UK), Spencer J. Sherwin (Imperial College London, UK)
Introduction
We review the technical innovations incorporated in the high-order incompressible Navier-Stokes solver that is part of the spectral/hp element platform Nektar++. We discuss the construction of a robust underresolved DNS (often called implicit LES) framework for complex geometries at high Reynolds numbers that typically arise in industrial applications. These problems require the use of unstructured high-order curvilinear (and possibly hybrid) meshes, as well as the application of regularisation techniques that help to stabilise the underlying numerics. We focus on (i) the complex high-order mesh generation step, (ii) the regularisation techniques required for numerical stabilisation, specifically a novel spectral vanishing viscosity approach, (iii) the physical accuracy of the results, and (iv) the computational performance of the overall simulation workflow. We then use as a practical example of this framework the high-fidelity simulation of a race car at a Reynolds number of 1,000,000 (based on the car length). The example shows that high-fidelity computations can help construct better aerodynamic solutions for industrial problems, provided that the (complex) geometry is represented correctly, accurate and stable numerical discretization schemes with low dispersion/diffusion errors are adopted, and numerics, physics and computer science are integrated efficiently under a single developmental umbrella.
High-order Solver for Underresolved DNS
Spectral/hp element methods (also known as high-order finite element methods) for computational fluid dynamics (CFD) simulations have become increasingly common over the last two decades in the academic community. Indeed, polynomials of higher orders within a single element offer a number of numerical advantages over standard low-order methods that still underpin and remain widely used in commercial fluid dynamics packages. From a numerical perspective, spectral/hp element methods (and high-order methods in general) exhibit far less numerical dispersion and diffusion than their lower order counterparts. Regarding turbulence simulations, flow structures can be more accurately represented during time integration and less prone to being artificially distorted and dissipated. Additionally, spectral/hp element methods methods also possess attractive computational properties. Contrary to low-order methods, which tend to lead to the formation of large sparse systems, high-order methods can exploit dense and locally compact elemental structures, which is more in line with modern computing technologies that require high degrees of arithmetic intensity to exploit the full potential of the hardware. For such methods to succeed in a commercial environment, a number of important and complex technical hurdles must be overcome – these are briefly reported in the following.
(i) Complex geometries. One of the key advantages of spectral/hp element methods over other high order approaches is their ability to adapt to complicated geometries by exploiting an elemental representation of the complex surfaces that characterize objects of interest especially in industrial applications. However, this comes with a significant challenge: to obtain an accurate numerical representation of a complex geometry, elements that connect to the geometry’s surface must be curved. This is an important problem to deal with, since a valid mesh that accurately represents the underlying geometry is a prerequisite to running simulations and exploiting the potential of high-order methods for challenging industrial and academic problems. Since one typically generates a coarse grid for LES simulations, this means that in regions of high geometric curvature, elements are prone to self-intersection. Additionally, the generation of boundary-layer grids, which are critical for the accurate prediction of e.g. skin friction drag, becomes highly challenging when considering extremely high-ratio elements found in high-Reynolds-number simulations common in industrial applications.
The first step in the process is the definition of the geometry of the computational domain in a way that ensures its geometrical accuracy and permits geometrical enquiries during the various mesh-generation stages. We will assume the geometry is given in a standard CAD format that supports a boundary representation description, such as the ISO 10303 standard, informally known as STEP (Standard for the Exchange of Product model data).
State-of-the-art methods for curved high-order mesh generation follow an a posteriori approach where a coarse straight-sided high-order mesh is generated from a linear mesh first and is then deformed to ensure its boundary conforms to the geometry. Our approach for the generation of boundary-conforming high-order curvilinear meshes employs the variational formulation described in reference [5] and implemented in the code NekMesh, part of the open-source Nektar++ framework [4].
(ii) Stability. Since Nektar++’s incompressible flow solver is based on the spectral/hp continuous Galerkin formulation, it lacks residual dissipation for advection dominated problems. This contrasts with discontinuous spectral element methods, which are naturally more robust for possessing a residual upwind dissipation. Still, even the latter can become numerically unstable at sufficiently large Reynolds numbers [1]. Numerical instability issues are basically twofold. On the one hand, the inherent dissipation of spectral/hp methods might be insufficient to stabilise (model-free) under-resolved DNS approaches. On the other hand, the non-exact quadratures often employed for the nonlinear terms present in the formulation can induce aliasing-driven instabilities and cause numerical divergence due to a build-up of energy in the high-frequency modes. The challenge is therefore to employ regularisation approaches that add a controlled amount of dissipation, consistent with the high-order approximation, and to apply dealiasing techniques to minimise errors due to non-exact quadratures. Although stability issues have been traditionally regarded as one of the main drawbacks of spectral/hp element methods, significant research has been devoted to these issues in recent years, so that numerical instabilities can currently be handled much more effectively.
We apply efficient polynomial dealiasing techniques to suppress aliasing-driven instabilities. For small-scale regularisation, we rely on a spectral vanishing viscosity (SVV) approach [9, 10] in contrast to explicit turbulence modelling. The novelty in our SVV operator is that it has been carefully designed to incorporate insights obtained from recent dispersion/diffusion eigenanalysis [6, 11]. This results in well-balanced dissipation characteristics that allow for the accurate simulation of test cases with higher Reynolds numbers. Since our SVV approach is built primarily upon numerical stability principles, rather than on physical modelling, we favour the term under-resolved DNS in lieu of the more popular implicit LES terminology, as we do not anticipate that our SVV-based approach incorporates turbulence physics in it. Instead, the relevant physics are expected to arise naturally from the governing equations, which are being solved at a greater degree of accuracy.
(iii)Physical accuracy. The absence of explicit LES modelling in the approaches considered can naturally be a point of concern. The main explanation currently available for the success demonstrated by underresolved DNS based on high-order spectral/hp element methods helps to illuminate this concern. Essentially, high-order hp discretisations have a superior resolution capability per degree of freedom and can be made stable with a numerical dissipation that affects only the small turbulent scales [2]. In other words, superior quality results can be achieved given the negligible numerical diffusion for the large and intermediate flow scales. Hence the turbulence physics contained in the Navier-Stokes equations can be more accurately captured for a broader range of scales. An explicit model, in contrast, would affect part of this range with modelling assumptions whose universality is questionable. The absence of an explicit model is particularly interesting for flows where transition is to be captured accurately, in which the negligible numerical dispersion/diffusion error typical of high order spectral/hp methods is especially important. This way physical instabilities are not artificially damped and are able to propagate longer without distortion. Nevertheless, there are still aspects that need be considered given that not every high-order method is equally suited for under-resolved DNS. One of those aspects concerns the distribution of dissipation in wavenumber/frequency space. For example, recent studies have pointed out that spurious effects can appear when the rise in dissipation in too sharp in Fourier space [1, 3]. One of the current challenges is therefore to adjust the numerics so that the shape of numerical dissipation in particular leads to even smaller effect on flow physics.
(iv) Computational efficiency.One of the main challenges in integrating higher-fidelity techniques into the industrial aerodynamic design cycle is the need for highly efficient implementations that can obtain solutions in a meaningful timeframe.
One of the advantages of higher order polynomial expansions is their ability to exploit high arithmetic intensities; that is, a greater number of floating point operations is performed for each byte of data retrieved from memory at higher orders than at lower orders. Although this naturally makes operator evaluations at higher order more expensive per degree of freedom, on modern computing hardware this effect frequently tends to be masked, as the cost of transferring data from memory to the compute unit tends to be far greater than that of performing floating point operations. In essence, this can make floating point operations nearly ‘free’ compared to the transfer of data.
However, the efficient implementation of the building block finite element operators that make up the discretised version of the incompressible Navier-Stokes equations, such as inner products or derivatives, still requires careful consideration. Even small changes in polynomial order can yield a large effect on performance due to the many dependent factors, including both the choice of hardware and the problem under consideration. Our recent work in this area [12] has focused on the development of techniques that can automatically determine the most efficient kernels for these operators at runtime.
High-order iLES of the Elemental RP1 road car
The RP1 [7], produced by the British manufacturer Elemental Cars since June 2016, is a high-performance, light-weight, road-legal vehicle that weighs 580 kg. It is equipped with a 320 bhp engine and accelerates from 0 to 60 mph in just 2.6 seconds. In this section, we will outline the use of Nektar++, alongside the developments highlighted in the previous section, to perform large-scale simulations to model aerodynamic performance of the RP1. In particular, Nektar++ has been instrumental in the design evolution process from the original configuration, pictured in Figure (2), which delivered 400 kg of downforce at 150 mph, to an optimised design delivering a large 25% improvement to 500 kg of downforce. These results have been validated using track data of the original design compared to the optimised design. We illustrate how high-order simulations have allowed us to identify potential design improvements to the RP1 car currently in production.
Simulation methodology
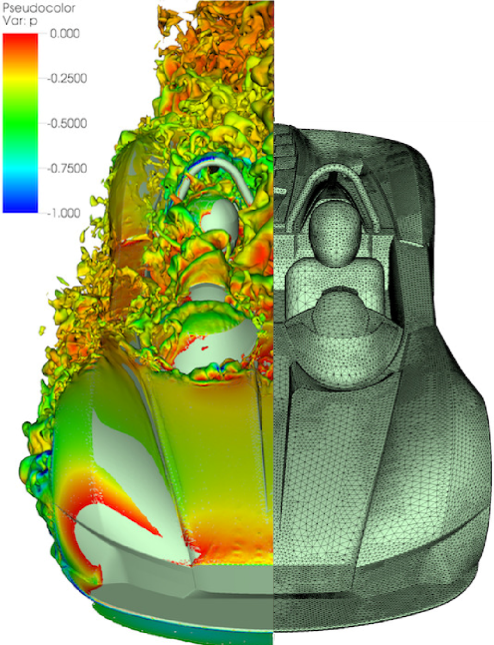
The hugely complicated nature of the geometry under consideration, which involves hundreds of CAD surfaces and thousands of edges, presented a significant test for the mesh generation process outlined in section 2. However, using the process outlined above, with use of CADfix and CFI for geometry repair and Star-CCM+ for boundary layer generation within NekMesh, yielded a valid curvilinear mesh suitable for computation. The high-order mesh used in this study ranged has approximately 3 million elements as the, comprising a combination of triangular prisms in the near-wall boundary layer region with 6 layers used to resolve separation accurately, and tetrahedra in the rest of the domain.
We note that to increase computational speed and reduce geometric complexity, a number of modifications were made to enable the simulation. Firstly, we adopt the standard practice of simulation of half of the car through the use of a symmetry plane. Additionally, the RP1 makes use of a unique double-diffuser design, with the presence of intakes and outlets on the body of the car. To model these accurately, these surfaces were extracted and a Poisson equation solved on the manifold to construct an appropriate velocity boundary field, using the techniques developed in [13]. A contact patch was added to accurately represent the road-tyre interaction, and rotational boundary conditions were applied to a simplified tyre geometry to model rotation of the tyre without the need for a moving mesh.
For the simulation itself, adopting a similar strategy to our previous simulations [8], we begin the simulations at a lower Reynolds number of Re = 10,000 where the Reynolds number is based on the length of the car L. The initial conditions are imposed impulsively so that u/U = 1, where U is a reference velocity, and all nonmoving surfaces are treated as no-slip boundaries. At the outflow, we impose the boundary condition developed by Dong et al. [14], which balances the kinetic energy influx through the outflow boundary condition

to prevent instability. The Reynolds number is then gradually increased by a factor of ten until the target Reynolds number is reached. Between increases, the flow is evolved for two convective time units to allow the flow to adapt to the increase in Reynolds number. The target Reynolds number in this case is 1 million, which we note is still lower than the experimental value of approximately 2 million. However, we note that this is still higher than other simulations which have been attempted of this type. This has been possible thanks to the new stabilisation techniques described in section 3.1. The simulations were run at a polynomial order 5 with a second order implicit-explicit timestepping. To increase the accuracy of the integration, a seventh order of quadrature was used. This meant that the meshes were generated at a higher order of P= 7 to ensure the elements were valid with this quadrature. The simulation were performed in parallel using 1000 to 4000 cores, depending on availability, of a SGI UV and took approximately 3 days to evolve the flow a convective length. Figure (3) shows the mesh used for the simulations and zero isocontours of total pressure coefficient, i.e. Cp0 = 0, coloured in pressure.
Design evolution
After performing an initial simulation of the original 2016 design, the high fidelity of flow simulations allowed unique insights to be made regarding the aerodynamic performance of the RP1’s complex geometric configuration. In particular, a number of important regions for aerodynamic optimisation were observed.
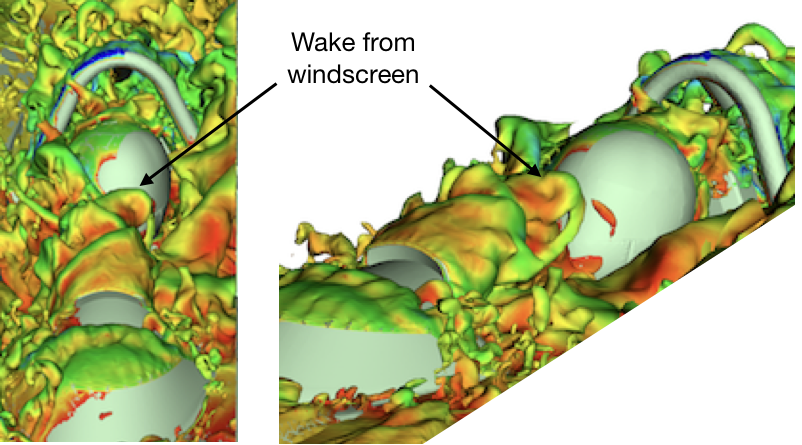
Simulations indicated the presence of an unsteady wake, which developed along the bodywork and impacted the occupant’s head and can be observed in Figure (4). This effect was observed and confirmed during track tests. Using the results of these simulations, a new windscreen was designed to eliminate this effect and greatly improve the driving experience. This new feature has been incorporated into a revised 2017 model and validated using track data.
As a result of the ability of Nektar++ to resolve laminar and transitional effects, we were able to obtain unique insight into the performance of the RP1’s double diffuser arrangements. We subsequently used this analysis to perform a redesign in the 2017 model, to boost downforce performance by 25% to a total of 500kg at 150mph. This additional performance was validated in track testing.
Finally, the roll hoop generated a much larger wake than expected, which contributed significantly to the drag of the car. The physics highlighted in Nektar++
simulations allowed for the development of an efficient high-performance aerodynamic package. This includes a rear wing design, informed by the results of the 2017 model, which will yield a predicted 1.2 tonnes of downforce for an anticipated 2019 model.
The analysis obtained during this design process was important from a variety of perspectives. Primarily, the use of Nektar++ has enabled a design evolution to a revised 2017 design with greatly improved performance, and was a key component of the design process of this upgraded car due to its ability to accurately capture the physics of highly loaded flow features. Additionally, however, the high fidelity of the solution has provided the insight and confidence required to successfully develop the RP1 without the use of traditional expensive wind tunnel testing.
Conclusions
This work demonstrates our significant progress in leveraging Nektar++ for the goal of moving high-order CFD from an academic to industrial tool, and some of the benefits that high-order methods can present to the industrial community. Significant developments had to be made in order to overcome obstacles in both mesh generation and solver technologies. However this project has driven and motivated developments in the Nektar++ framework which have moved us much closer to a viable tool in industrial CFD. A detailed description of these and further aerodynamic improvements on the design of the car resulting from the use of high-order iLES will be described elsewhere.
Acknowledgments
This work has benefited from the technical support and design insight from Elemental Cars and from access to large HPC resources provided by SGI. We also would like to thank Mark Gammon and his group at ITI Global for providing us with a license to the program CADfix and its CFI interface, and for their technical help and support.
Partial financial support was provided by EPSRC under the Platform Grant PRISM: Underpinning Technologies for Finite Element Simulation (EP/L000407/1) and by the EU Horizon 2020 project ExaFLOW (grant 671571). M. Turner acknowledges the support of EPSRC and Airbus under an Industrial CASE studentship.
References
[1] R. C. Moura, G. Mengaldo, J. Peiró, and S. J. Sherwin, “On the eddy-resolving capability of high-order discontinuous Galerkin approaches to implicit LES / under-resolved DNS of Euler turbulence,” Journal of Computational Physics, vol. 330, pp. 615–623, 2017.
[2] R. C. Moura, S. J. Sherwin, and J. Peiró, “Linear dispersion-diffusion analysis and its application to under-resolved turbulence simulations using discontinuous Galerkin spectral/hp methods,” Journal of Computational Physics, vol. 298, pp. 695–710, 2015.
[3] A. R. Winters, R. C. Moura, G. Mengaldo, G. J. Gassner, S. Walch, J. Peiró, and S. J. Sherwin, “A comparative study on polynomial dealiasing and split form discontinuous Galerkin schemes for under-resolved turbulence computations,” Journal of Computational Physics, 2018.
[4] C. Cantwell, D. Moxey, A. Comerford, A. Bolis, G. Rocco, G. Mengaldo, D. Grazia, S. Yakovlev, J.-E. W. Lombard, D. Ekelschot, B. Jordi, H. Xu, Y. Mohamied, C. Eskilsson, B. Nelson, P. Vos, C. Biotto, R. M. Kirby, and S. J. Sherwin, “Nektar++: An open-source spectral/hp element framework,” Computer Physics Communications, vol. 192, pp. 205–219, 2015.
[5] M. Turner, J. Peiró, and D. Moxey, “Curvilinear mesh generation using a variational framework,” Computer-Aided Design, vol. 103, pp. 73–91, 2018.
[6] R. C. Moura, S. J. Sherwin, and J. Peiró, “Eigensolution analysis of spectral/hp continuous Galerkin approximations to advection-diffusion problems: Insights into spectral vanishing viscosity,” Journal of Computational Physics, vol. 307, pp. 401–422, 2016.
[7] Elemental Cars, “The Elemental RP1.” http:// elementalcars.co.uk/the-rp1/, 2018.
[8] J.-E. W. Lombard, D. Moxey, S. J. Sherwin, J. F. A. Hoessler, S. Dhandapani, and M. J. Taylor, “Implicit large-eddy simulation of a wingtip vortex,” AIAA Journal, vol. 54, no. 2, pp. 506–518, 2016.
[9] G. S. Karamanos and G. E. Karniadakis, “A spectral vanishing viscosity method for large-eddy simulations,” Journal of Computational Physics, vol. 163, no. 1, pp. 22–50, 2000.
[10] R. M. Kirby and S. J. Sherwin, “Stabilisation of spectral/hp element methods through spectral vanishing viscosity: Application to fluid mechanics modelling,” Computer Methods in Applied Mechanics and Engineering, vol. 195, no. 23, pp. 3128–3144, 2006.
[11] R. C. Moura, S. J. Sherwin, and J. Peiró, “Spatial eigenanalysis of CG and DG methods with insights on solution quality and numerical stability,” research report, Imperial College London, 2017.
[12] D. Moxey, C. Cantwell, R. Kirby, and S. Sherwin, “Optimising the performance of the spectral/hp element method with collective linear algebra operations,” Computer Methods in Applied Mechanics and Engineering, vol. 310, pp. 628–645, 2016.
[13] C. D. Cantwell, S. Yakovlev, R. M. Kirby, N. S. Peters, and S. J. Sherwin, “High-order spectral/hp element discretisation for reaction–diffusion problems on surfaces: Application to cardiac electrophysiology,” Journal of computational physics, vol. 257, pp. 813–829, 2014.
[14] S. Dong, G. E. Karniadakis, and C. Chryssostomidis, “A robust and accurate outflow boundary condition for incompressible flow simulations on severely-truncated unbounded domains,” Journal of Computational Physics, vol. 261, pp. 83–105, March 2014.



