Authors: Neil D. Sandham, Roderick Johnstone, Christian T. Jacobs
Direct numerical simulation (DNS) of turbulent flow is highly accurate, capable of resolving all turbulence length scales with the numerical grid. However, applications of DNS are limited due to the sheer computational cost of the approach, since the number of grid points scales very strongly with the Reynolds number (e.g. Re(37/14) for aerofoil boundary layer flow [1]).
Large eddy simulation (LES) is a cheaper approach, typically using about 1% of the number of grid points required for DNS. However, smaller scales become important near walls, so LES often becomes "wall-resolved" in practice and the strong scaling issue remains. Wall-modelled options are attractive, but such an approach relies heavily on a wall treatment / reduced order model.
In light of the issues surrounding accurate turbulence simulation, we have developed a new heterogeneous modelling approach (as part of Work Package 1) which reduces the cost of simulating high Reynolds number flows whilst retaining solution accuracy by combining LES with quasi-DNS (QDNS) simulations. Essentially, the whole domain is simulated with the coarse-grid LES, and the equivalent of wall functions is provided by an array of non-space-filling QDNS 'blocks' mounted to the walls (see Figure 1). Here we consider a three-dimensional channel flow setup at Reynolds number Re-tau = 4200 [2].
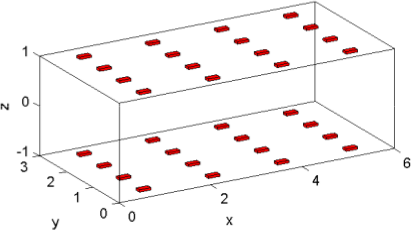
The approach is capable of resolving and coupling together the different turbulence structures; the LES resolves the large scale motions, while the QDNSs resolve the near-wall regeneration cycle of streaks and small vortices. The two components are coupled together as follows: the wall shear stresses from the QDNSs act as a boundary condition to the LES, and the bulk velocity from the LES drives the QDNSs and enforces a constant mass flux.
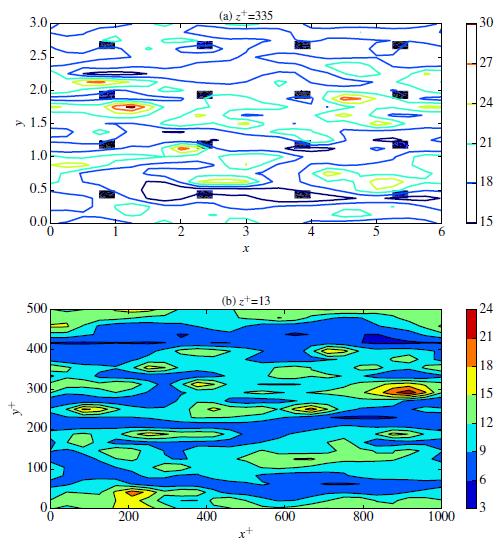
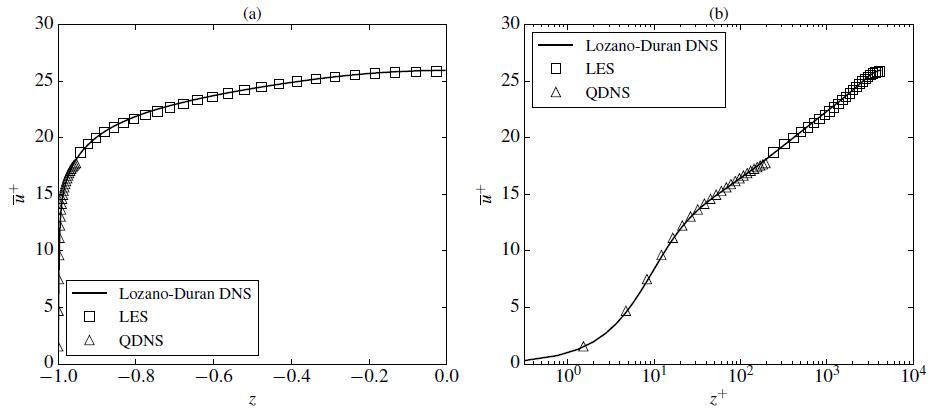
The visualisation of the streamwise velocity field in Figure 2 shows the development of near-wall streaks and vortices as expected. The combined approach was able to accurately capture the mean streamwise velocity profile (Figure 3) whilst using only ~0.02% of the number of DNS points used by [2], thereby demonstrating its efficiency benefits.
For more information, please see the paper by [3].
References
[1] H. Choi, P. Moin (2012). Grid-point requirements for large eddy simulation: Chapman's estimates revisited. Physics of Fluids, 24(1), doi: http://doi.org/10.1063/1.3676783
[2] A. Lozano-Duran, J. Jimenez (2014). Effect of the computational domain on direct simulations of turbulent channels up to Re-tau=4200. Physics of Fluids, 26(1), doi: http://doi.org/10.1063/1.4862918
[3] N. D. Sandham, R. Johnstone, C. T. Jacobs (2017). Surface-sampled simulations of turbulent flow at high Reynolds number. International Journal for Numerical Methods in Fluids, 85(9):525-537, doi: http://doi.org/10.1002/fld.4395



