Author: Christian Jacobs, University of Southampton

Explicit finite difference (FD) algorithms lie at the core of many CFD models in order to solve the governing equations of fluid motion. Over the past decades huge efforts have been made by CFD model developers throughout the world to rewrite the implementation of these algorithms, in order to exploit new and improved computer hardware (for example, GPUs). Numerical modellers must therefore be proficient not only in their domain of expertise, but also in numerical analysis and parallel computing techniques.

As a result of this largely unsustainable burden on the numerical modeller, recent research has focussed on code generation as a way of automatically deriving code that implements numerical algorithms from a high-level problem specification. Modellers need only be concerned about writing the equations to be solved and choosing the appropriate numerical algorithm, and not about the specifics of the parallel implementation of the algorithm on a particular hardware architecture; this latter task is handled by computer scientists. A separation of concerns is therefore created, which is an important step towards the sustainability of CFD models as newer hardware arrives in the run-up to exascale computing.

As part of the ExaFLOW project, researchers at the University of Southampton have developed the OpenSBLI framework [1] ( https://opensbli.github.io ) which features such automated code generation techniques for finite difference algorithms. The flexibility that code generation provides has enabled them to investigate the performance of several FD algorithms that are characterised by different amounts of computational and memory intensity.

Performance Evaluation

An investigation into the run-time performance of 5 different FD algorithms, outlined below, was undertaken. All algorithms solved the unsteady compressible Navier-Stokes equations in the context of the Taylor-Green vortex problem [2]. A fourth-order central differencing scheme was used in conjunction with a low-storage RK3 timestepping scheme.

• BL: The Baseline algorithm is similar to typical handwritten CFD codes in the sense that all derivatives in the RHS of each equation are evaluated and stored in memory as arrays of grid point values (also known as 'work arrays').
• RA: The Recompute All algorithm, in contrast to the BL algorithm, involves replacing the continuous derivatives in the RHS of each equation by their respective finite difference formulas during the code generation stage. All RHS derivatives are therefore recomputed at each timestep.
• SN: The Store None algorithm is similar to RA, but in the loop over grid points each RHS derivative is evaluated as a single process-/thread-local variable, rather than a global-scope grid-sized work array.
• RS: In the Recompute Some algorithm, only the first derivatives of the velocity components are stored in work arrays while all other derivatives are replaced by their finite difference formulas (as per the RA algorithm).
• SS: In the Store Some algorithm, only the first derivatives of the velocity components are stored in work arrays while all other derivatives are evaluated and stored as process-/thread-local variables.

The implementation of each of these algorithms as C code was generated automatically by specifying certain flags in the high-level problem specification, thereby highlighting the flexibility that OpenSBLI offers to the numerical modeller.

The results from each algorithm were successfully validated against existing Taylor-Green vortex DNS data [3]. Scaling runs were then performed, for 500 timesteps, on a single node (24 cores) of the UK National Supercomputing Service (ARCHER). It was found that the Store Some (SS) algorithm was the fastest algorithm in terms of run-time, as shown in the table below:

The plots below also show good strong and weak scaling of the SS algorithm up to several tens of thousands of cores.

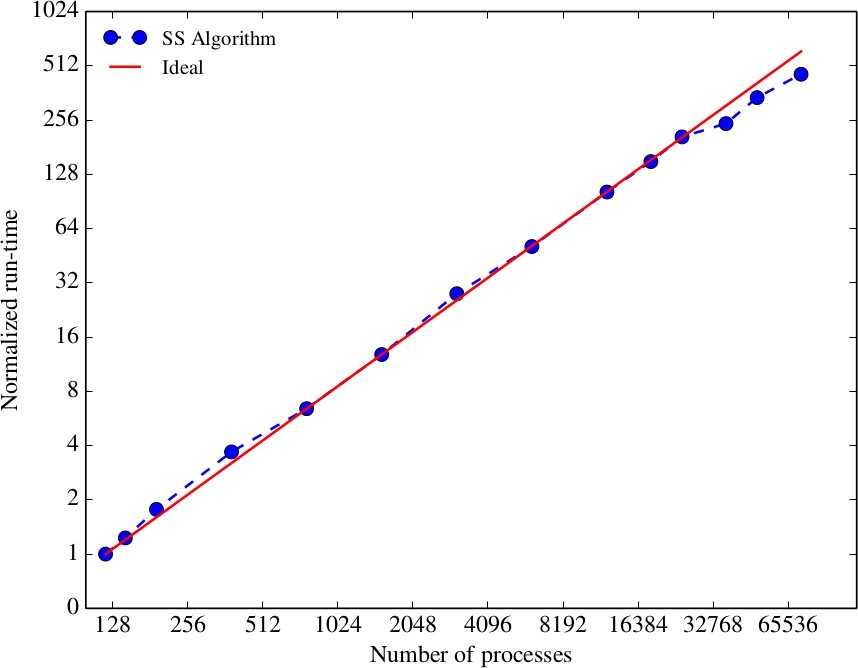
Figure 1: Strong scaling of the SS algorithm on ARCHER up to 73,728 cores using 1.07 x

10^9 grid points. The run-time has been normalised by that of the 120-process case. Image from [4].

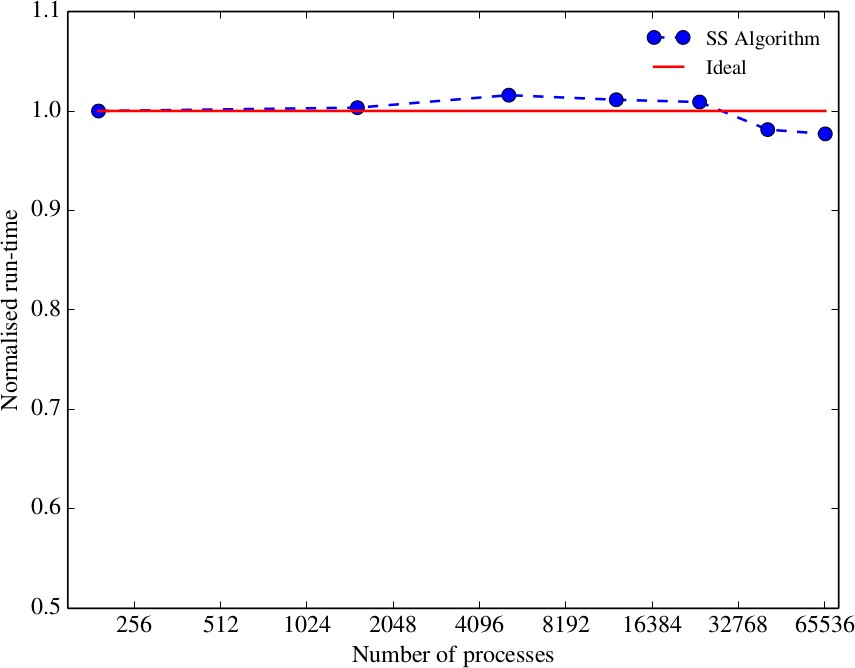
Figure 2: Weak scaling of the SS algorithm on ARCHER with 64^3 grid points per MPI

process up to 65,856. The results have been normalised by the run-time from the 192-

process case. Image from [4].

The run-time for the BL algorithm, used in many existing CFD codes, was approximately 2 times larger than all the other FD algorithms. BL is the most computationally-intensive algorithm here, but the least memory-intensive, while the best-performing algorithm (SS) is somewhere in between these two extremes. Through the use of code generation, model developers can readily change the computational and memory intensiveness of the underlying numerical algorithm to determine the best performing algorithm for a given choice of hardware architecture. Further details of this work can be found in [4].

If you want to find out more about this topic please contact Satya P. Jammy, Christian T. Jacobs or Neil D. Sandham at the University of Southampton. 

References 

[1] C. T. Jacobs, S. P. Jammy, N. D. Sandham (2017). OpenSBLI: A framework for the automated derivation and parallel execution of finite difference solvers on a range of computer architectures, Journal of Computational Science, 18:12-23, doi: http://doi.org/10.1016/j.jocs.2016.11.001

[2] J. DeBonis (2013), Solutions of the Taylor-Green Vortex Problem Using High-Resolution Explicit Finite Difference Methods, 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition (February 2013), 1-9. doi: http://doi.org/10.2514/6.2013-382

[3] Z. Wang, K. Fidkowski, R. Abgrall, F. Bassi, D. Caraeni, A. Cary, H. Deconinck, R. Hartmann, K. Hillewaert, H. Huynh, N. Kroll, G. May, P.-O. Persson, B. van Leer, M. Visbal (2013). High-order CFD methods: current status and perspective, International Journal for Numerical Methods in Fluids, 72(8):811–845. doi: http://doi.org/10.1002/fld.3767

[4] S. P. Jammy, C. T. Jacobs, N. D. Sandham (In Press). Performance evaluation of explicit finite difference algorithms with varying amounts of computational and memory intensity. Journal of Computational Science, doi: http://doi.org/10.1016/j.jocs.2016.10.015