Author: Adam Peplinski, KTH

Computational Fluid Dynamics (CFD) relies on the numerical solution of partial differential equations and is one of the most computationally intensive parts of a wide range of scientific and engineering applications. Its accuracy is strongly dependent on the quality of the adopted grid and approximation space on which the solution is computed. Unfortunately for most interesting cases, finding the optimal grid in advance is not possible and some self-adapting algorithms have to be used during simulation. One of them is Adaptive Mesh Refinement (AMR), which allows to dynamically modify both grid structure and approximation space and provides the possibility to control the computational error during the simulation and to increase the accuracy of the numerical simulations at minimal computational cost.

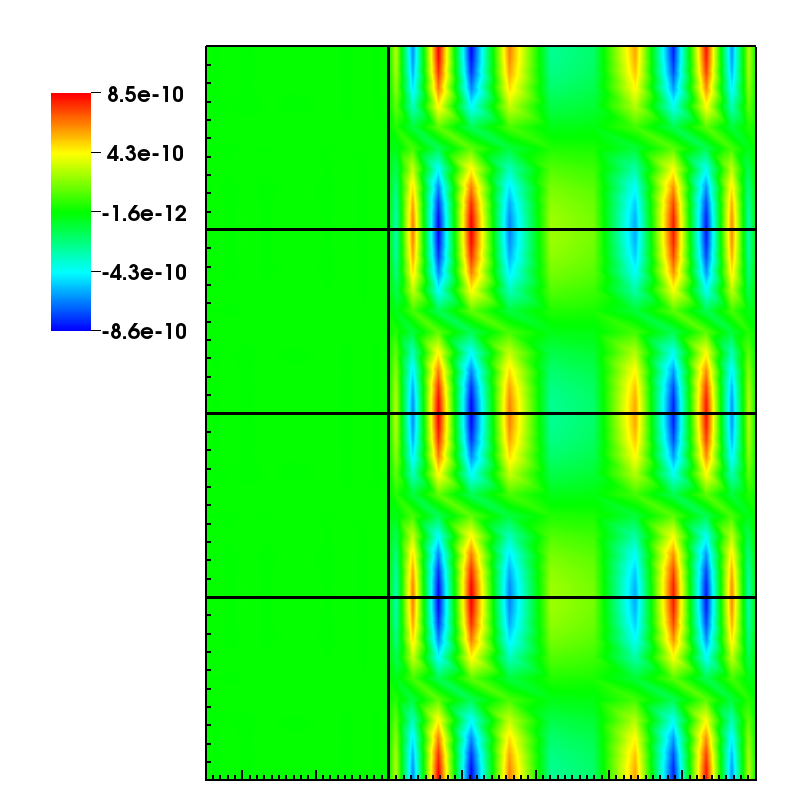
Figure 1: The error of the stream-wise velocity component for the conforming mesh. Black lines show element boundaries.

Within ExaFLOW we aim at implementing AMR in the Spectral Element Method (SEM) code Nek5000. The SEM discretisation is based on a decomposition of a computational domain into a number of non-overlapping, high-order sub-domains (elements). There are two major ways of introducing AMR for SEM: adaptive approximation space modification, i.e. increasing polynomial order in individual elements (p-refinement), and adaptive grid modification, i.e. splitting the element into smaller ones (h-refinement). H-type refinement of the advection-diffusion equation was implemented by us into Nek5000 within the EU project CRESTA [1]. We used the p4est library for the management of the AMR tree grid and the ParMETIS library for mesh partitioning. Mesh refinement was performed based on spectral error indicators [2].

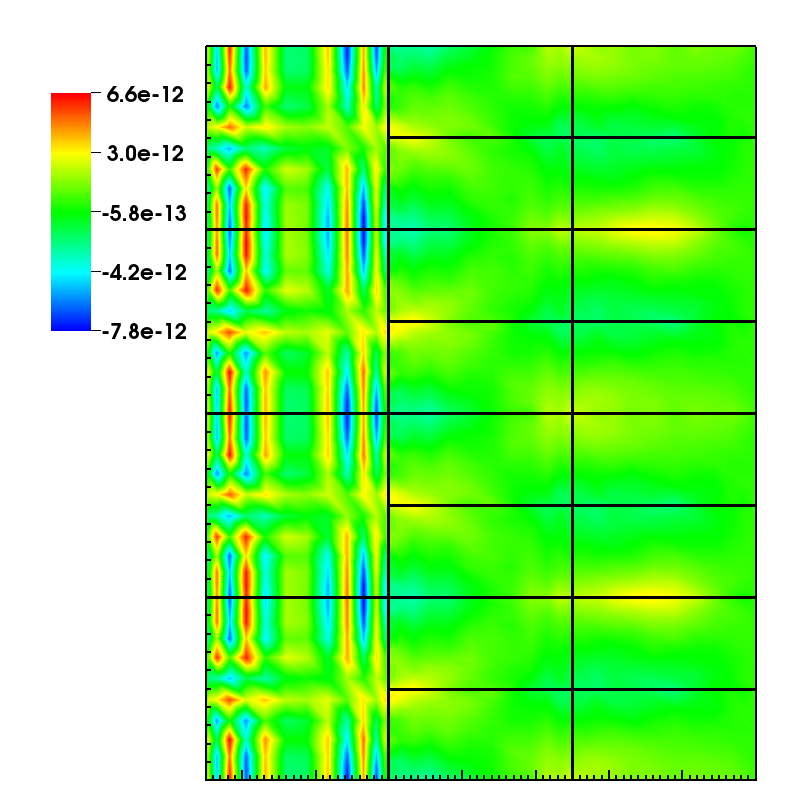
Figure 2: The error of the stream-wise velocity component for the nonconforming mesh. Black lines show element boundaries.

Currently we extend our previous implementation to the full nonlinear Navier-Stokes equations for incompressible flow. In this case one has to perform costly pressure calculations which require efficient preconditioners for nonconforming meshes to limit number of iterations. At present we have upgraded the pressure preconditioner for steady state calculation and tested it with the Kovasznay flow [3] which is the two-dimensional flow-field behind a periodic array of cylinders. It is a perfect testing case as it provides an analytical solution that allows to calculate the exact error of the numerical solver. The error of the stream-wise velocity component for the unrefined and refined simulations is presented in figures 1 and 2 respectively, and shows the error reduction by two orders of magnitude for the refined grid. In our next steps we will continue with upgrading the pressure preconditioner for time dependent flows.

If you want to find out more about this topic feel free to contact Adam Peplinski of the KTH at This email address is being protected from spambots. You need JavaScript enabled to view it. .

References

[1] Peplinski, A., Fischer, P. F., Schlatter, P. Parallel Performance of H-type Adaptive Mesh Refinement for Nek5000, in Proceedings of the Exascale Applications and Software Conference 2016, Stockholm, Sweden
[2] Mavriplis, C. A Posteriori Error Estimators for Adaptive Spectral Element Techniques, in Proceedings of the Eighth GAMM-Conference on Numerical Methods in Fluid Mechanics,333–342. Vieweg+Teubner Verlag, Wiesbaden, 1990
[3] Kovasznay, L. Laminar flow behind a two-dimensional grid, Proc. Cambr. Philos. Soc. 44, 58–62, 1948